Brad DeLong has a blog post at the Equitable Growth blog called "Scene-Setting for the Policy Discussion: The American Economy Stumbles." The post is far too pessimistic about America's economic performance, especially over the period from 1980-2000. Here are a few points where I think Brad gets it wrong.

Brad's thesis is the following:
The American economy has done badly over the past generation or so.
This is not to say other economies have done better: The American economy remains among the richest in the world. However, given the economic lead America had a generation ago, it really ought to still be well ahead of the North Atlantic pack, and it no longer is.
I think this is a defensible thesis, if A) you define "a generation" as 15 years, and B) you deny that Solow convergence should take place at the higher levels of country income.
But in any case, I do not think that Brad successfully defends the thesis!
First, I think Brad dramatically understates the progress Americans experienced during the years from 1980 through 2000:
Across most of the income distribution Americans today are little if any better off than their predecessors back in 1979...Yes, today Americans have remarkable access to incredibly cheap electronic toys. But those are a small part of expenditure, and the costs of securing the standard indicia of middle-class life–a home in a safe neighborhood with good schools and a short commute, college for the children, assurance that a major illness will not lead to bankruptcy, a secure and reasonably-sized pension–have all become more costly relative to incomes. This shift is astonishing: For 150 years before 1979 Americans had confidently expected that each generation would live roughly twice as well in a material sense as its predecessor, not find itself struggling against the current to stay in the same place.
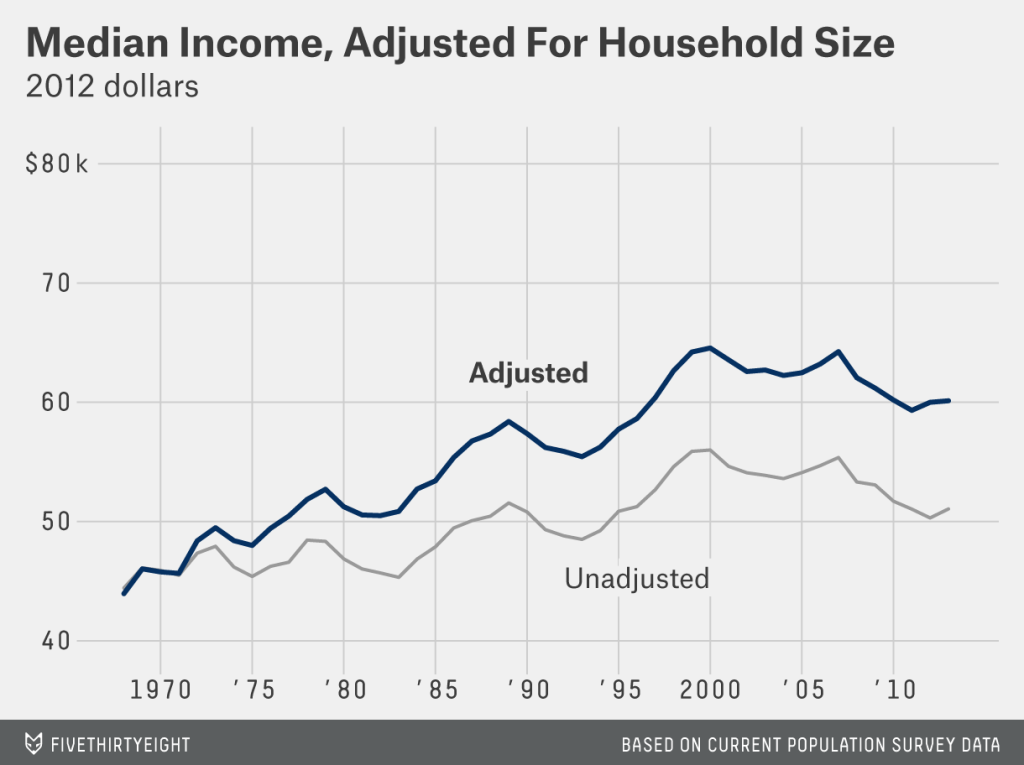
First of all, here is a picture of American median household income:

As you can see, even if we do not adjust for household size, the median American household experienced a substantial rise in income from the 1979 business cycle peak through the 2000 business cycle peak - around a 17% rise. But if you adjust for household size, the increase is around 23%, from a higher base.
Of course, this does not account for A) age, and B) composition. American households got much older from 1980 to 2000, and old people do not work much. Also, there was a boom in low-skilled immigration in the 1990s, which, although it boosted U.S. total GDP and was good for us overall, did tend to reduce the median income through composition effects.
Now, it is true that these figures also do not account for A) home production, and B) leisure. The entry of women into the workforce, which was not fully matched by male exit, meant that parents were spending less time with their children. And leisure did temporarily decline during the 1990s, after holding steady in the 1980s (then soared in the 2000s). So that mitigates the rise in living standards over the 1980-2000 period. But the truth is that in terms of purely material standard of living, the average American was substantially better off in 2000 than in 1980.
Anyway, Brad claims that the price of housing has gone up. He also claims that people (even well-off people!) live in smaller houses than in 1979:
The rest of the top 5% are about as rich as they might have expected. They have traded smaller houses and more burdensome commutes for more lavish vacations, cheap electronic toys, and greater social order.
House size, in fact, went up substantially between 1980 and 2000:
Also, I would argue that rent, not the price of a house, is the key measure of the cost of housing. Bubbles in the price-to-rent ratio merely offer households the opportunity for arbitrage. Here, via Mark Thoma and Robert Shiller, is a graph of real rents in the U.S.:
So even as house size soared, real rents stayed flat over the latter part of the 20th century. To me, that looks like a large increase in the standard of living of the average person.
What about the rest of Brad's "standard indicia of middle-class life," whose cost has supposedly soared? Regarding "a home in a safe neighborhood," the massive crime decline in the U.S. during the 1990s probably helped the lower and middle classes a lot more than the upper classes. Regarding "good schools," the performance of U.S. public schools remained flat or risen slightly relative to other countries, and in terms of NAEP scores, over 1980-2000 (and since). As for "burdensome commutes," this is true: average commute time increased by about 40 minutes per week from 1980 to 2000, and has been flat since 2000 - but this is an area in which new technology may be especially game-changing, since cell phones, texting, games, and podcasts/audiobooks make commuting much more fun. I get more "reading" done on my commute than during any other time.
It is certainly true that college has gotten much more expensive, health care bankruptcies have become more common, and pensions have become less generous (though this last is partly a function of Americans' increased consumption levels as a percentage of disposable income).
But then again, life expectancy has increased by about 5 years since 1980. That is not nothing. And many social indicators, including teen pregnancy and drug abuse, have decreased substantially.
Of course, all these numbers are just statistics - what about the lived experiences of Americans? Over the last two decades of the 20th century, Americans owned more cars, consumed more calories, had more TVs in their house, had bigger houses (as discussed above), and spent much less of their income on food, clothing, and shelter. These are things that mainly affect the marginal utility of the poor and middle class.
Brad's other main contention is that the U.S. is not doing well relative to other rich countries:
If you want a single set of numbers to keep in the front of your mind to understand America’s relative position today, you cannot do better than those in the figure below, copied from the Credit Suisse Global Wealth Report:
The median American has only about $45,000 to his or her name, and wealth inequality as measured by the gap between the average and the median wealth is greater by far than in the typical rich country–only Sweden comes close. A generation ago it would have been ridiculous to even consider that the typical middle-class or working-class American might not lose if switched with the typical inhabitant of Australia or Italy or Japan or Finland or Singapore. It is not so ridiculous at all today.
Median net worth, of course, depends heavily on things like asset prices; the number for the U.S. dropped by more than half as a result of the housing bust. Other countries, like Canada, did not experience a housing bust. Also, net worth depends heavily on age, and the U.S. is younger than many of the countries listed above us in the median wealth ranking.
But more fundamentally, is median wealth the proper measure of living standards? Wealth is a function of savings rates, and savings rates depend on consumption levels, which are a choice. During the 1980s and 1990s, Americans chose to consume more of their income than our peers in most rich countries (though this has recently reversed itself in some cases, e.g. in Japan). If you look at median disposable income, the U.S. was ahead of every other rich country except Canada in 2010, despite some convergence:
As you can see, the U.S. was still ahead of the North Atlantic pack in 2010. Only Canada caught up (and we'll see how well that holds now that oil prices have crashed). We still comfortably beat Sweden, Germany, Britain, the Netherlands, and France. Japan is not listed, but the pattern is the same.
If this income disparity continues to hold, then the U.S. can climb back up the median wealth rankings whenever it feels like it - just save more out of disposable income. (Note: This graph does NOT prove that U.S. median standards of living are higher than these other countries, since those numbers are before transfers, and also do not take into account things like transport, crime, pollution, health, nice weather, or good fashion sense. But it DOES show that Americans could climb up the wealth rankings over time, if they wanted to.)
So in conclusion: Bad Brad! In 2000, you believed that American economic policy and the American economy, though far from perfect, had been largely a success (right?). It's understandable to think the 15 years since then have been a big disappointment - they have! - but why should that cause you to revise your evaluation of the period from 1980 to 2000? Do you think that we are now paying for excesses we enjoyed in that period, and that our prosperity increases during that period were thus illusory? I don't think you think that. So don't succumb to excessive pessimism!


Nice, agree.
ReplyDeleteAlso: why are crime and "bad schools" even included in a list of failures of "the economy?" I don't think either of these things would change much even if we doubled everybody's income. (That aside from the fact that they have generally gotten better, not worse, since 1980.)
Wow, Noah, if this comment is representative of the people who agree with you, then I sincerely doubt that your post is correct.
DeleteI agree with ed. Just look at the late 1960s U.S. and Malaysian v. Indonesian standardized test scores.
Deleteremove the low IQ students and school performance shoots way up. if you compare US Koreans with Koreans in Koreans, our Koreans score higher. But academic surveys lump everyone together. By ignoring the role biology plays in school performance, one may be mistaken to believe that our public schools are only churning out ignoramuses , when in fact, America has some some of the smartest and most talented students in the world; it's just they they are mixed in with the dull ones, weighing down the average.
DeleteRemove the poor people and the average wage shoots way up! Remove the bad comments and the average quality of the comments rises! Profundity!
DeleteEd, economics is very much to do with solving the issues of crime and bad schools and essentially all of *societies' issues*. Economics, and the success of an economy, is concerned with the allocation of resources to maximise societal welfare. GDP, income etc are used as proxies to assist measurement, they are not the end in itself.
If you define economics strictly in terms of maximising everyone's income, then you are flat out wrong. Zimbabwe had everyone's income rise by 231,000,000% under Mugabe. It's not the world's most successful economy.
Fangz, you know ed was talking about real income, not nominal. You also know that if American dumb students were educated in any part of Europe instead of here, it is highly unlikely they would have become any smarter.
Delete"Even as house size soared, real rents stayed flat over the latter part of the 20th century...that looks like a large increase in the standard of living of the average person."
ReplyDeleteThe BLS, or any economist measuring rents, is trying to hold the quality of housing constant. So house size should have no effect on rents. Thus, if real rents have been flat, that means that housing has made no contribution to living standards.
One important reason for this is that productivity growth in homebuilding is typically very low, or even negative. So this has been a pretty big failure of the US economy.
The increase in house size is a physical quantity; it means that people have more stuff, period!
DeleteVery good point (I've made it many times myself). Also those larger homes have more amenities; more bathrooms, built in vacuum systems, spas, patios and landscaping.
DeleteAlso, prior to 2000 I couldn't challenge Brad DeLong's arguments unless I flew down to Berkeley. Today I can with a few minutes typing, and a flick of my wrist.
Or I could, before he started deleting them.
Noah: Nice. We should always jump back and forth between median and average during a conversation without making any attempt to be consistent...
DeleteI thought you economists were required to take statistics?
However, given the economic lead America had a generation ago, it really ought to still be well ahead of the North Atlantic pack, and it no longer is.
ReplyDelete------------------
But it it. I usually agree with brad on things like debunking inflation fear mongers and the efficacy of monetary policy, but he's wrong here. Adjusted for inflation, the US economy has done better than all its peers since 2009. America is not in decline, never was, and is doing better than ever.
have you adjusted for increase in debt?
Delete"just as a bad cold leads to pneumonia, so over-indebtness leads to deflation" - Irving fisher
DeleteIrving fisher has shown that paul krugman is clinically retarded
that's not an issue. free money. Despite the debt being at record highs, thanks to low rates and the global flight to safety to reserve currencies, adjusted for inflation, the US is paying record low interest on its debt, going as far back as the 1940's:
Deletehttp://www.marketminder.com/img/US-Federal-Debt-Interest-Payments-as-a-Percent-of-GDP2.jpg
5:34: If you are working 40 hours a week and you borrow more money than you can service during those 40 hours, you are over-indebted. If you aren't working at all and borrow money to start a job that will let you work 40 hours a week to service the debt, you aren't over-indebted.
DeleteMedian disposable income after taxes is going to penalise countries with high tax rates and large public sectors/public service provision, even though the latter presumably matter a great deal for the median.
ReplyDeleteDoes the Luxembourg IS data 1/ allow for transfers (as well as taxes); have an estimate of public spending "consumed" by the median household?
That's a good point! It's really hard to measure the quality of government services...
DeleteEspecially given that in many countries, health insurance is embedded in taxes.
ReplyDeleteHard to say if and when I'll have time to really read this, but just in case, don't forget ginormous positional externalities, and that, of course, it's not just averages, it's risk, and the world has gotten a whole lot riskier for people, and that really hurts expected utility. Want facts to back it up -- see Yale's Hacker's The Great Risk Shift, and the recent, Chasing the American Dream, by Washington St. Louis sociologist Mark Rank.
ReplyDeleteBut in general,there's a powerful advantage always to living in a later time of more advanced technology and medicine (if you can get access to it). But compared to where we could be without a generation of right wing dominance starving public investment and sending inequality into the stratosphere,...
Ok, yes, there were other forces sending inequality soaring besides the dominance of the right, but the right said, great! lets make it even a lot worse, where the left and center would have taken steps to diminish it, and diminish it greatly in the case of the Democrats, if they could truly get what they want, things like universal free high quality pre-school, college, healthcare, etc.
Delete"Of course, this does not account for A) age, and B) composition. American households got much older from 1980 to 2000, and old people do not work much."
ReplyDeleteUnless they have to , to keep their heads above water. Average hours worked per household rose about 10% between 1980-2000. For two-parent families , it rose even more , explaining the entirety of their income gains :
http://www.brookings.edu/blogs/jobs/posts/2011/07/~/media/Research/Images/C/CF%20CJ/chart1.jpg
Look at wages or income for the full-time median male and it's flat for 3+ decades , unless , perhaps , you choose to look at the median banker or CEO.
http://4.bp.blogspot.com/-Z0gCWP--Dzw/UCvdTH9-ePI/AAAAAAAAF0E/QZaXw4U338E/s1600/us-men-real-median-income-with-recessions-1947-2010.PNG
Your graph of adjusted hh income starts in 1970 , a common trick used by those who want to hide the fact that incomes and living standards doubled for EVEYONE in the 30 years prior , in line with productivity. That was the "Golden Age". Since then , anything but golden - more like brown , and stinky.
Your post suggests a different name for the current age - "The Age of Propaganda in Service of Plutocrats".
Well done.
All you're doing is picking demographic slices that did worse than the average, and treating those slices as if they're all that matters. And you're doing it because you've reached a conclusion ahead of time - "PLUTOCRATS HAVE TAKEN ALL OUR MUNNY, RAGE RAGE" - and you go looking for ways to slice the data to back that up.
DeleteBut look at my post. It's very comprehensive. Not all the things I quote point in the same direction. Some things I quote detract from my case. Is that just me being very sneaky with my propaganda, pretending to be fair-minded while advancing the wishes of the Plutocrats? Or am I actually trying to get a good picture of what happened to the American middle class, while you're just spouting polemic?
You're exactly where DeLong was in 2000 , when he too was pimping for plutocracy. Now his hero Larry Summers has reversed course , possibly feeling guilty for his contributions to the current state of affairs , so DeLong joins in with his transparently ambivalent mea culpa.
DeleteThe middle class is swirling ever deeper into the drain as we type - 401ks are being tapped prematurely , family heirlooms are being hocked , all in a futile effort to maintain an already too-modest lifestyle , given this country's riches.
You'll see how stupid this post looks in years to come , but I doubt you'll admit it , or regret your stupidity : " Hey , I was just maximizing my utility , in a plutocracy."
Dammit, you're right. I see it so clearly now. How could I have been so wrong??
DeleteMocking people who disagree with your take as screaming "RAGE RAGE" is a bit immature, don't you think? As the other Anonymous poster above notes, hours worked needs to be taken into account just as much (if not more so) than household size (since it's hard to separate cause and effect when it comes to the relationship between choosing to having kids and income). And, when it comes to hourly wages, it's pretty clear that the increases experienced by median income workers have been minuscule over the past 35 years. http://www.stateofworkingamerica.org/chart/swa-wages-figure-4b-real-hourly-earnings/
DeleteThe Median Household Income figure can be misleading, especially since the evidence is that individual wages didn't adjust much across the board aside from the late 1990s. Most of the gains in household income came from an increase in the number of two-income households, I'd bet - even after you figure in the rise of single-parent households.
ReplyDeleteSure. The entry of women into the workforce surely must have held down wages. It also must have decreased the total amount of home production, which doesn't get measured in GDP.
DeleteThis comment has been removed by the author.
DeleteIn general I agree but that median per capita income after taxes data is deeply suspicious. The US is not wealthier on average than Scandinavia especially not Norway by a long shot. How does Norway have less than $20k median per capita income after tax? What is that some kind of hyper PPP? Why exclude all taxes when comparing living standards, doesn't that inflate the measured status of countries with less public services eg healthcare? I'm calling Big Big Big BS on that bottom chart.
ReplyDeleteHere are some thoughts of mine on the household income statistics (one of my most successful posts):
ReplyDeletehttp://richardhserlin.blogspot.com/2014/02/important-points-that-are-rarely-made_2.html
I don’t know where Brad got his house size statistic; I’ve also seen that average house size went up a lot.
ReplyDeleteBut you can’t compare home buying and home renting like that; it’s too much apples to oranges. Very very few families think arbitrage when buying starts to get a lot more expensive than renting compared to the past. They’re just very different markets in the minds of most families. There are just so many people set on living in their own house, and grossly grossly overestimating how good an investment purchasing a home is. I’m amazed, especially in the more expensive areas, like LA and San Francisco, how crazy more expensive buying is than renting in about the same area.
I have heard many academics talk about this topic. Listening to academics compare renting to homeownership always feels like walking into a parallel universe. Academics are typically overeager to apply a superficial symmetry to a situation, and very few or no academics have really tried to understand the fundamental differences between the two. An owned home and a rented home are not merely 2 different ways to get the same good; they are 2 fundamentally different goods.
DeleteYeah, I found this quote of Noah's hilarious:
Delete"Bubbles in the price-to-rent ratio merely offer households the opportunity for arbitrage."
While technically true, in practice I do not think this happens often enough for any sort of an impact.
"Those with lower incomes and less education have, at best, seen hardly any rise in life expectancy at age 65; in fact, those with less education have seen their life expectancy decline." -- Kruggie
ReplyDeleteat: http://www.nytimes.com/2013/11/22/opinion/krugman-expanding-social-security.html
Brilliant web research (mostly googling I assume). I learned a huge amount from the data you found. Also brilliant post.
ReplyDeleteHowever there is one booboo. The last graph you present is "median per capita income *after taxes*" but then you typed "since those numbers are *before taxes* and transfers". Also, by the standard definition "income includes" transfers, income without transfers is usually called "market income."
I'm not saying you are wrong Noah, but I don't think the data you rallied is sufficient.
ReplyDelete1. I don't understand why you bring the 2000 peak into it. Brad talks about *today*, not 2000 at the height of the dot-com bubble. By eye, comparing today to 1979, an increase from ~49 to ~50 on the unadjusted values qualifies for "little if any better off." The household size adjustment might help, but it's not clear how meaningful it is in this context.
2. The graph you pulled about house sizes is about the size of new single-family homes. Here's the problem - that's about new houses being constructed. That says little about houses people actually live in! If those big houses were being constructed on the site of demolished larger ones, if the graph is actually due to a reduction in the construction of houses on the low end of the market, or if they are simply sitting empty while everyone moves into flat-shares in city centres, then the average size of homes could easily diminish. That graph is essentially tangential to Brad's point.
3. Disposable income as you define it is utterly useless. Why? Because what is 'disposable' changes in definition. For example, healthcare spending comes out of disposable income for americans - you buy your medical insurance from your post-tax income. In the UK, however, it's paid out of taxation. Healthcare is a *lot*.
Suuure, the US individual could build up net worth by declining any medical insurance. But to use that as an argument why he's better off? Questionable.
"median wealth the proper measure of living standards"
ReplyDeleteOf course not, this is what drives me nuts about the debate, it's what you can buy with it.
"It is certainly true that college has gotten much more expensive,"
Well, yes - but shouldn't this be obvious? The things that have become relatively more expensive - e.g. education and health care - are the things where labor productivity has been slowest. We still educate people largely the way we educate them 800 years ago, in classrooms. It takes about the same amount of time to teach calculus as it did in 1950, except more people want to learn it..
Housing, we cannot mention housing without mentioning that the Rent is Too Damn High - housing expensive in many pockets of the country because we go out of our way to restrict supply (zoning restricts how many units per acre you can build in a lot of places, while there are a lot of regulations that make it cost ineffective to redevelop on existing land).
And, we cannot mention infrastructure & transportation without mentioning how expensive per mile it is to build in the US, compared to our peers in other countries. It has gotten to be absurd how long it takes to review projects, and time is money.
Seems to me, mostly this is a labor productivity story: Agriculture and manufactured goods have become really cheap because we have made tremendous productivity gains. Health care and education we have not. Those things have become relative expensive.
What I really want to know from these college professors is how they are working on making education more efficient. Human brain interface so we can learn calculus and biochemistry in days rather than weeks? Then the cost of education goes way down, and we can train more doctors so the cost of health care goes down. And when everything is cheaper, like oil, I have a lot of money left over to buy other stuff, or go on vacation.
There is a lot of nit-picking in the comments which I suspect comes from pre-formed political/economic views. If one looks a Noahs post more generally and openly, his args. support the view that we are too pessimistic. "The Plutes stole all the money!" sounds good, but is somewhat inaccurate. My wife and I lived the generation Noah describes (both of us blue collar) and we were able to own a home, educate our children, enjoy the decrease in crime rates (the psychological security of a better world is incalculable), own the tech miracles of the age and establish a sense of security for our (possibly) advanced years. Our children are doing better than we were at the same point in our lives (they don't have a college education by their own choice). They have good jobs, are buying their own homes, drive nicer vehicles than we did and are smarter and more educated than we were (mainly due to the aforementioned tech miracles). There exist economic and social inadequacies in our society, but I agree with Noah, they are not as ubiquitous as many progressives claim. "So don't succumb to excessive pessimism!" Nice post, Noah.
ReplyDeleteTo that I say:
Deletehttp://i.imgur.com/GheT1x1.jpg
So your point is that reality is not an accurate harbinger of, reality? We should all be doing LSD and "talking with our minds"?
Deletehttp://youtu.be/2ftvh9eWkAc
I'm saying that you using your family as evidence for Noah being right or wrong, is essentially entirely meaningless. I have no doubt that your experience is real, but it's a tiny tiny piece of reality. We should be taking a broader view.
DeleteHow else would I be able to judge whether Noah is right or wrong? Is there some non-prosaic level of knowledge I am missing here? Statistics are interesting, but does a lot of sand make a beach a beach, or is a beach a piece of land which lays near a body of water? As for experience being "a tiny, tiny piece of reality", good luck with that one. Taking a broader view is always good, but the judgements one makes are very much personal and relative to experience. That is the reason scientists conduct experiments. Perhaps you are saying you don't know of anyone else who has managed to thrive in lower-middle class America in the last 30 years? That can't be right.
ReplyDeleteYou should be able to judge by looking at the reasonableness of his arguments, and whether there's any holes in them. The fact that there's a personal nature to judgements is true, but that means efforts have to be made to avoid and minimise this subjectivity.
DeleteExperiments with a sample size of 1 are worthless - even if representative. And you aren't: most people who did really really badly and lost their homes won't be reading this blog in the first place. So the readers here are inherently more likely to be the lucky ones.
No one says *all* middle class people are doing badly. Just that many are.
First, Noah has a reasonable argument with few "holes in them", in my "judgement". Avoiding subjectivity is an oxymoron, no matter the subject matter.
DeleteSecond, I did lose my home and farm and do read this blog, but this was poor financial judgement, not ill-luck.
Third, a sample size of 1, "even if representative", means what? That it is representative?
Fourth. Noahs post did not pretend everyone was doing great, he was saying that there exist widespread anomalies which contradict the "we all gonna die! (poor and oppressed)" mentality.
Fifth, I don't think I am "middle class" or "doing badly". My wife and I, in a good year make 40-45K. If that makes me too lucky to read Noahs opinion, he will certainly tell me to get my ass out.
It sounds like DeLong's post was the first in a series. The first chapter is a call to arms, with suggested solutions coming in future posts. Of course the first chapter has to be a bit sensational in order to make it worth writing and reading the rest. That's good salesman ship, which I think Noah has done in the past in the name of readership.
ReplyDeleteSmith's retort is that things were bad, but not really bad. Maybe we can score a point for Noah (maybe not once DeLong replies). But what are we to do, public policy wise, with the bad but not really bad prognosis? Noah isn't advocating, but entertaining the blogosphere. I look forward to the rest of DeLong's posts.
Summary and other comments
ReplyDeleteIn much of the country, especially the prosperous sections housing is not affordable for those in most income brackets
Medical care has grown enormously more expensive as fewer and fewer jobs include medical care. (ACA is helping with this despite Republican opposition)
Fewer and fewer jobs are including pensions, and at the same time Republicans are attacking Social Security again.
College costs even at State supported institutions are rocketing in price. At one time Republican were great supporters of affordable education. No more.
When housing, medical, education, and pensions are becoming more unaffordable for the three and possibly four lower income quintiles, "Houston, there is a problem".
I'm confused on why Noah compared 1979 to 2000 when DeLong seems to be aiming at 2015. (I'm confused generally at why progressive economists start comparisons 1979ish instead of 1973, the last year wage "equality.") I compare 1973 to present -- even adjusted for household size (w/o adjusting for hours) that leave the median a big 20% ahead after per capita income grew 66% ...
ReplyDelete... and going down. The dip isn't a glitch -- it is a product of total de-unionization (imagine how poor Germans would be in 2015 if they never had unions); no matter if everything else worked right. The top 10% used to get most of the growth. Now the top 1% get 95% -- seemingly not a glitch.
If the latter is permanent (or gets worse!), then, by the time per capita GDP grows 50% the top 1% will have 75% of the 150%, etc.
The federal minimum wage is almost $4 lower than in 1968 -- after per capita income doubled.
The real minimum needs line for a family of three is more like $1000/wk according to the 2001 Ms. Foundation book Raise the Floor (table 3-2 on p.44). Yet the median wage is $26,000 -- that's all those people we come in contact with everyday at one of their working class jobs. A $15 minimum wage would only shift 3.5% of GDP -- easily doable. Ditto for paying people enough to work across the board.
100,000 of what I would guess are 200,000 Chicago gang age males are in street gangs I would assert because they wont work for half what the minimum wage should be. UC Berkeley political scientist who spent 9 years on the streets of 5 NY and LA ghettos discovered that the schools there don't work because too many of the students (and teachers!) don't see anything enough rewarding waiting for them in the labor market to make it worth the extra effort.
So we have not done too well -- but it only takes a reasonable, shall we say, re-sharing of incomes (permanent basis) to straighten it all out. Which means re-unionization.
This comment has been removed by the author.
DeleteThe beginning of quick re-unionization? -- what a Democratic issue! -- couldn't just leave my post above hanging with no suggestion of a practical way back. :-)
Delete* * * * * * * * * *
States could conceivably pass legislation that would allow the federal RICO statute to be applied to "consultants" conspiring with management to deny workers the use of the federally prescribed right to vote to certify a union -- by firing any and all union proselytizers. Currently this economically ruinous extortion may not be considered a criminal offense. It does violate administrative law rules and if employers are found guilty they must pay (a relatively small) compensation to the worker for lost time (not a penalty).
If a state makes this deprivation of the most core human economic -- and political -- rights into a state crime, then, the federal RICO statute could be applied to perpetrators within that state. Their crime fits under "extortion" for purposes of such a statute (it's just possible it already fits today). The feds used RICO to chase the mob out of our unions -- time for RICO to chase the union busting mob out.
Of note for Canada, median income was stimulated by a housing bubble that has yet to burst (middle skill jobs) and an energy supercycle (more middle skill jobs) that caused the former and that is now apparently over - housing is next. My country turned into a one-trick pony, and now that our manufacturing base is gone, we're in for a rough ride despite the CAD tumble.
ReplyDeleteYour suggestion that Americans could somehow "just save more out of disposable income" raises the age old question of what are they supposed to save with? Food and manufactured goods prices are down, but housing, medical care, education and a host of other expenses are up. Until the 1980s, a house cost 600 hours of work a year. Then it shot up to 800 and has risen more since. That leaves a lot less for savings, especially since available work hours have decreased. There was a reason all those women went to work in the 1980s and it wasn't just that Ronald Reagan was a feminist.
ReplyDeleteThere's also the issue of job security, pension security and a host of other changes over the past decades. People used to take government jobs at lower salaries because of the civil service job security. Now, non-government workers have no job security and lower salaries. How did this happen? Also, aside from Social Security which has been under relentless attack, what sort of retirement security does anyone have? (Granted, if you are really rich and lose your money in some dumb investment scam, the government will make good, but very few of us are that rich.)
I don't think that 23% rise over a 35 year period is all that much to brag about.
Noah,
ReplyDeleteMore people working per home and a temporarily decline in leisure during the 1990s have lead to a purely material standard of living increase of these households. Great.
Your efforts for showing the half-full part of the proverbial glass are commendable. But your post suffers from wishful thinking in some parts of the text.
Definitely, median wealth is not a worse measure than median disposable income (see Anonymous 5:46 PM).
You can do a better job. This is not your best post.
You should see Elizabeth Warren's work on the collapse of the middle class:
ReplyDeletehttps://www.youtube.com/watch?v=akVL7QY0S8A
http://harvardmagazine.com/2006/01/the-middle-class-on-the-html
"Today the median income for a fully employed male is $41,670 per year (all numbers are inflation-adjusted to 2004 dollars)—nearly $800 less than his counterpart of a generation ago. The only real increase in wages for a family has come from the second paycheck earned by a working mother. With both adults in the workforce full-time, the family’s combined income is $73,770—a whopping 75 percent higher than the median household income in the early 1970s. But the gain in income has an overlooked side effect: family risk has risen as well. Today’s families have budgeted to the limits of their new two-paycheck status. As a result, they have lost the parachute they once had in times of financial setback—a back-up earner (usually Mom) who could go into the workforce if the primary earner got laid off or fell sick. This “added-worker effect” could buttress the safety net offered by unemployment insurance or disability insurance to help families weather bad times. But today, a disruption to family fortunes can no longer be made up with extra income from an otherwise-stay-at-home partner.
Income risk has shifted in other ways as well. Incomes are less dependable today. Layoffs, outsourcing, and other workplace changes have trebled the odds of a significant interruption in a single generation. The shift from one income to two doubled the risks again, as both Mom and Dad face the possibility of unemployment. Of course, with two people in the workforce, the odds of income dropping to zero are lessened. But for families where every penny of both paychecks is already fully committed to mortgage, health insurance, and other payments, the loss of either paycheck can unleash a financial tailspin. ...
"Why are so many moms in the workforce? Surely, some are lured by a great job, but millions more need a paycheck, plain and simple.
It would be convenient to blame the families and say that it is their lust for stuff that has gotten them into this mess...But is this argument true? If families really are blowing their paychecks on designer clothes and restaurant meals, then the household expenditure data should show them spending more on these frivolous items than ever before. But the numbers don’t back up the claim. ...
So where did their money go? It went to the basics. The real increases in family spending are for the items that make a family middle class and keep them safe (housing, health insurance), that educate their children (pre-school and college), and that let them earn a living (transportation, childcare, and taxes). ...
Combine changes in family income and expenses, and the biggest change of all becomes evident—on the risk front. In the early 1970s, if any calamity came along, the family devoted nearly half its income to discretionary spending....But the position today is very different. Fully 75 percent of family income is earmarked for recurrent monthly expenses. Even if they are able to trim around the edges, families are faced with a sobering truth: every one of those expensive items—mortgage, car payments, insurance, childcare—is a fixed cost. ...In other words, today’s family has no margin for error. There is no leeway to cut back if one earner’s hours are cut or if the other gets sick. There is no room in the budget if someone needs to take off work to care for a sick child or an elderly parent. Their basic situation is far riskier than that of their parents a generation earlier. The modern American family is walking a high wire without a net."
Another dreadful post devoid of thought.
ReplyDeleteHow did you value the loss due to increased supply of labour?
How did you measure the loss associated with reduced pension provision?
Increased prison population?
Not only have we gotten all these technological goodies, but have you seen the bean spice mix packets they've put out recently ? They're awesome.
ReplyDeleteParents are spending more time with their children! Don't let the haters hate
ReplyDeletehttp://www.pewresearch.org/data-trend/society-and-demographics/parental-time-use/