
Everyone (hopefully) knows there are many measures of risk in financial markets. The most commonly used example is volatility, but if your returns are skewed, you might want to focus only on the lower tail of the distribution, and if your losses are fat-tailed, you might want to use something like the Conditional Tail Expectation. But no matter what measure you use, you can't really measure risk.
Before I say why, let me contrast risk with something you sometimes can sort of measure: return. Actually, measuring return is very hard, because to measure the overall return of your portfolio, you have to measure the value of your assets. And that's hard. Just think of American banks, when they tried to value their mortgage-backed assets in the middle of the financial crisis. It was nearly impossible to mark assets to market, because there was no market - no one was buying. But "mark to model", i.e. using some theory to value the assets, was no better; it was rightly denigrated as "mark to myth".
As if that weren't enough, there's also the matter of price impact or slippage. When you try to sell stuff, the price will tend to change. That's a transaction cost, and it's an unpredictable transaction cost. So if I have a hundred tons of gold, it's hard to know how much I could get for that gold if I sold it all, even if I know the current price.
But if you liquidate all your investments, you can get cash, and since cash is the unit in which we denominate value (no "money is a bubble" stuff, please!), you can know your nominal return in that case...unless you count non-salable assets like human capital in your "portfolio", of course. And your real return, which depends on future inflation, is never quite calculable.
But compared to risk, return is peanuts to measure. Why? Because risk is all about counterfactuals.
Return can't be known in advance, obviously, but if you can mark to market and if you ignore price impact, you can measure your return after the fact. Not so with risk. Risk not only can't be known in advance, it can't be known in retrospect either. Suppose I buy GM stock, hold it for a year, and then sell. How much risk did I incur over that period? First of all...who cares? It's over and done. But even if I did care, I couldn't know, because what actually happened to my asset reveals little about what might have happened.
For example, the realized volatility of the asset over that holding period tells me little. First of all, it didn't end up mattering for my eventual return. Second of all, I might have been able to time the ups and downs, buying when it was cheap or selling when expensive. And knowing how likely I would have been to successfully time the returns is incredibly difficult.
But also, the realized volatility doesn't tell us how likely volatility was to change over that period. See, volatility changes. Over at his blog Keplerian Finance, Stony Brook applied math prof and long-time hedge-fund maestro Robert Frey does a quick calculation of S&P volatility, and identifies what look like distinct regimes. He bins them up into the following picture:
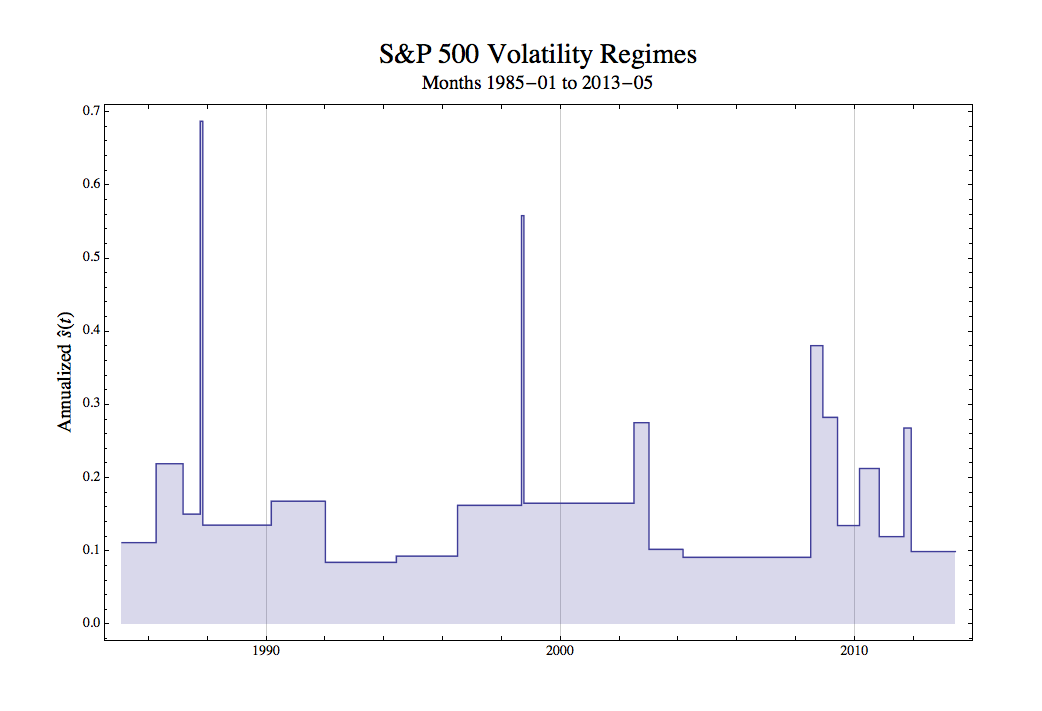
As you can see, volatility is mostly constant, but has a few extremely spiky spikes. Whatever is causing those spikes, they're too rare and too irregular to get a good idea of how likely you are to hit a spike in any given year.
So suppose your GM stock didn't have a ton of volatility over the year in which you held it. No spikes. But what were the chances of one of those spikes happening over that year? You don't really know. So that means you don't really know if whatever return you ended up making was justified by the risk.
You'll never know how closely you dodged a bullet.
One interpretation of this is that there's always true Knightian uncertainty in the world. Another is that there's only risk (i.e. probabilities are fixed), but we'll always have great difficulty estimating it from data. The difference is mostly philosophical; effectively, those are the same thing. Andrew Lo goes into a lot more depth on the topic in this famous paper.
Now this doesn't mean we can know nothing about risk. Obviously we can know something about it - measures like volatility or conditional tail expectation are useful. But not only will we never know everything about risk, we'll never know how much we know about it; at any time, our quantitative measures of risk might be getting more informative or less informative, as Frey's graph shows pretty clearly.
So how should we react to the unknowability of risk? Should we simply assume that the "true" distribution is so fat-tailed that we should avoid taking chances as much as possible? Probably not, since over many stretches of time, people who assume that "true" risk is small (distributions are thin-tailed) will sometimes end up being correct for a very long time. And for that very long time, the risk-ignorers will prosper much more than the risk-suspecters.
In fact, there is no optimal solution. Sometimes we'll guess there's more risk than there actually is, and sometimes we'll guess less. And we'll never know which of our guesses were right, or whether we just dodged a bullet we never saw.
I think this is why it pays to 1- run 'what if' scenarios regularly...
ReplyDelete... and 2- have an idea of the underlying world to see whether you're nearing "risky" situations.
Now, that last bit seems preposterous. "Economists predicted 8 out of the last 3 recessions" kinda stuff. And, to a degree, it is.
For example, I think it is not a bad rule of thumb to consider that the most/longest something went up, the closer you are to a reversal.
Say, present-day markets have been running higher and higher on rather weak fundamentals (getting more and more pricey as a consequence) and possibly because of QE. VIX was 12.5 a week ago... It wouldn't strike me as a bad time to either buy some VIX calls (strike 22?) and/or get a bit more cash in the portfolio...
Now, it's true I might have said the same thing 3 months ago too and, as you mentioned, there is an opportunity cost to worrying.
OTOH, surviving bad times is not to be underestimated if you're not a too-big-to-fail institutions or a hot trader with a nice Rolodex, forever able to find new suckers to hire you...
"Now, it's true I might have said the same thing 3 months ago too and, as you mentioned, there is an opportunity cost to worrying." - yep, you could have been like me and actually acted, and then mistime the exit.
DeleteBrilliant analysis of the implications of true uncertainty in markets. This brings many of the recent objections (Mandelbrot, Taleb) with the older objections (Minsky, Keynes) into a clear position.
ReplyDeleteOne aspect I would like to explore is the idea: "Whatever is causing those spikes, they're too rare and too irregular to get a good idea of how likely you are to hit a spike in any given year." This statement seems correct in practice, but perhaps not necessarily correct in theory.
In theory, if you held the conditions of the market constant for a prolonged period of time, you could gather enough data to get a reasonable handle on these unusual events. However, in practice, the conditions of the market change too significantly in a short period of time to make such long-term data ever practicable to collect. Therefore, we have no counterfactual and they are unknowable in practice.
As to how we should react. The first step must be widespread acknowledgement that risk is practically unknowable and uncertainty is inherent in finance. From this acknowledgement of initial ignorance, we can take more conservative and well-founded assumptions to reestablish what can be known. As I have argued recently, if we do not acknowledge that risk is immeasurable, new models will always fall short of the old models.
http://distilledmagazine.com/economic-models-analysis/
Excellent article. I am glad to see such clear analysis on this subject.
While I agree with your sentiment I disagree with your argument.
ReplyDeleteI think the issue is, as far as I can see, there is no coherent consensus on what risk is, which I think is a point you make, and as a result there can be no single measure of "risk".
For example, in Lo and Mueller we have that risk is a quantifiable randomness but uncertainty is unquantifiable. My issue with this is that I am uncertain as to the distance between Edinburgh and New York, but this is nothing to do with randomness. While I am only highlighting a semantic issue, it is none the less pertinent.
For me, science is not very good at distinguishing a lack of information from "randomness". Even Taleb does not appreciate the significance of Black Swans in scholastic philosophy: a Black Swan event is not a rare event but one that exhibits God's will in confounding the laws of nature. In the context of Economics I think Morgenstern captured this in his observation that
"always there is exhibited an endless chain of reciprocally conjectural reactions and counter-reactions. This chain can never be broken by an act of knowledge but always through an arbitrary act — a resolution" (reference cited in my post http://magic-maths-money.blogspot.co.uk/2013/07/moralised-markets.html)
i.e. economics is only dynamic because agents do the unexpected. This can be seen as a problem of information, but I would suggest however good we get at psychology, economic agents will always be one step ahead of the scientists.
For me this is at the root of the problem with randomness, which is beyond the problem of agreeing what risk means.
Two points.
ReplyDelete"it didn't end up mattering for my eventual return"
I suspect you didn't really mean to say this. For a holding period of a year, some sort of geometric growth is more reasonable than arithmetic growth. And when growth is geometric, increasing volatility lowers returns. For example, for GBM, the ensemble expectation of growth is the drift mu but the time expectation (i.e. the expectation of an individual investment) is mu - 0.5 sigma^2, by Ito's lemma. It doesn't matter that assets don't really follow GBM - any geometric process will have the same qualitative properties. But you must know this quite well.
And speaking of qualitative, while I intuitively want to agree with your main point, you have not done enough to demonstrate it here. It is not sufficient that individual risks cannot be measured for risk as a whole to be immeasurable; it is also necessary that we cannot rank risks, and say which is greater. (I think that would also be true but it is harder to demonstrate.) So long as probabilities can be ranked, that suffices to induce a "qualitative probability structure" not very different from an ordinary probability scheme. There is an essay by Patrick Suppes meditating on some remarks by de Finetti which demonstrates this.
I suspect you didn't really mean to say this. For a holding period of a year, some sort of geometric growth is more reasonable than arithmetic growth. And when growth is geometric, increasing volatility lowers returns.
DeleteOf course. What I meant was: "Given that my portfolion value begins at point A and ends at point B, who cares by what path it got there?"
Oh dear. I think you were in a stronger position before you defended yourself.
DeleteNo, I think you just don't understand what I'm trying to say. Which is of course my fault for not explaining well.
DeleteTry this: Given V(0) and V(T), the value of my portfolio at the time I start investing and the time I cash out, my utility does not depend on V(t) for any 0<t<T.
Does that make sense now?
How about the price of risk? I've wanted to kill that one off for some time.
ReplyDeleteHi Noah:
ReplyDeleteNice post. However........and please correct me if I am wrong:
(1) The primary reason you conclude that return is easy to measure is that from period-to-period we deal in a market where price changes are determined linearly in return. and that is all we care about. This is mostly true.
(2) But today, we have pretty well-developed and liquid markets in 2nd and higher order moment of a distribution: variance swaps on equities, rates and Fx, Correlation swaps and skewness and kurtosis contracts (the French banks and Citigroup are very active). In some sense of course, there is no such thing as the realized distribution, unless you pre-state it to be Gaussian and "pin" the two moments on expiration date.
In this context, if you are long an equity, you are long return (or 1st moment), short risk (or variance). If you wanted to flatten out the 2nd moment, you could buy an appropriate amount of variance swaps (how much? Well I am sure you can figure that one out!))
I think you are arguing here a broader point, something Post-Keynesians have been arguing after Keynes: you cannot build a coherent theory of the economy if you assume ergodicity and rational expectations and throw away radical uncertainty.
ReplyDeleteVery true!
DeleteSo are you a Post Keynesian now? Forget about getting published ;)
DeleteNah, I'm starting my own school of economic thought. Post-Keynesianism is yesterday's news.
DeleteGo get'em!
DeleteIt is often argued that Knight and Keynes in 1921 co-invented the distinction between risk and uncertainty, although it was Knight who first used those terms. This is tied to the fact that the view Keynes put forth in his Treatise on Probability was more nuanced, subtle, and complicated, and more relevant to the points you are making here, Noah, along with people like Lo and Mueller.
ReplyDeleteFor Knight there were the two categories: quantifiable risk and unquantifiable uncertainty. Keynes allowed for more intermediate forms. "Radical" Keynesian uncertainty resembles Knightian uncertainty, there is no probability distribution at all. At the other extreme there is not only a probability distribution, but it is easily known and categorized, as in the canonical case of flipping a "fair" coin (let us avoid the problem of how we know a coin is "fair" or not).
But there are these intermediate cases, several of which have been mentioned. So, there may be a probability distribution, but for a variety of reasons, including simply not being able to make enough relevant observations, we cannot determine it with any degree of certainty. Or then there is the matter that opened the discussion, that even if the distribution is known, there may be competing ways of characterizing its riskiness or volatility. Variance works fine if one has a Gaussian distribution, but other measures may be more appropriate when there is skewness or kurtosis. This latter case is what Taleb refers to as "grey swans" to contrast with the black swans of deeper and truer uncertainty.
After a natural disaster, insurance premiums go up, even if there's no reason why the disaster should alter our estimate of risk.
ReplyDeleteStock markets seem to have the same property: they compensate investors for past losses, not for risk.
A natural disaster can increase the demand for insurance and decrease the supply - hence higher prices until the insurance industry rebuilds its capital and homeowners become complacent.
DeleteShouldn't insurance premium reflect the actuarial fair price, and not the demand aspect?
DeleteCan an economist/finance/quant weigh in on this? I'm thinking that Max has a good point. Seems to me that insurance premiums overreact to the disaster?
Usually there is a *market hardening* after an adverse event. Insurance is priced by people and people get spooked. Capital doesn't flow perfectly freely and no one knows what actuarialy fair rate is. If actuaries use historical data, which is primarily how rates are calculated, then a recent big loss impacts those calculations.
Deletewe'll never know how much we know about it
ReplyDeleteCall Rumsfeld, he'll straighten this all out.
you may want to read up on GARCH during your winter break,
ReplyDeletethanks for posting and enjoy the break!
This is a category mistake.
DeleteNoah's article is about *measures* of risk. GARCH is a method used to *estimate* a measure of risk.
Still, GARCH is a handy thing to know.
you may want to read up on GARCH during your winter break
DeleteWinter? Are you in Australia or New Zealand??
Asset allocation (and re-balancing) uses simple arithmetic to address risk. this is not very adventurous (nor yields highest returns) but it is simple and modestly safe. And for most people owning an affordable house, along with an affordable 30 year mortgage is again not adventurous but almost always safe. (not all that many Detroits)
ReplyDeleteit's not that difficult to determine:
ReplyDelete1)what price you'll get when you sell and
2) your return
3)the proceeds
1. is determined by looking at the bid of the bid/ask spread. but for a very big order you will get a lower price and to determine this price you may need a more complicated method , but for a highly liquid stock and a modest sized order your execution price is going to be the quoted 'bid', give or take a few tenths of a percent.
2. your % returns is simply the final capital divided by the starting. easy. nominal is just = final - starting
3. the proceeds of a sale is determined by taking the integral of the price function from t_o to t_1 upon the addition of your sell orders to find the mean value and multiply this by the number of shares sold. this can be hard but like 1., for the majority of cases its just the order size times the bid price.
Very interesting post. I think there are different ways to define risk vs uncertainty.
ReplyDelete1. A situation that is well defined, the probability distribution is fixed and known, but the outcome is unknown.
2. The situation is not well defined, the probability distribution is fixed, but unknown. The outcome is unknown.
3. The situation is not well defined, the probability distribution is constantly changing and unknown at any given time. The outcome is unknowable.
#1 Can be called risk.
#2 Can be called epistemological uncertainty.
#3 Can be called ontological uncertainty.
Really, you can call these conditions whatever you would like but they are all different. #2 is closer to how Knight defined uncertainty where #3 is closer to how Keynes defined uncertainty.
A situation is "well defined" when the variables that affect the probability distribution are known.
In an uncertain situation, the variables are not know as humans possess imperfect knowledge. The difference between #2 and #3 goes one step further. Not only are the variables unknown, but even if they were known, the relationships the variables have with one another is subject to change.
#2 suggest that if humans possessed perfect knowledge or had a machine that allowed this (advanced computers), all variables in the present could be known and their relationships with one another could be revealed. If this was possible, uncertainty involving the future could be quantified. With perfect knowledge uncertainty can be reduced to risk. Risk can be managed.
#3 suggest that even if one possesses perfect knowledge of all variables and their relationships with one another, uncertainty could still never be quantified. This is because the nature of the variables is subject to change and their relationships with each other are not fixed. Furthermore, new variables can come into existence. Therefore, even with perfect knowledge, uncertainty is not reducible.
See:
Keynes and Knight on uncertainty – ontology vs. epistemology
http://larspsyll.wordpress.com/2012/07/29/keynes-and-knight-on-uncertainty-ontology-vs-epistemology/
As others have noted, this is essentially the starting point of Keynes's analysis.
ReplyDeleteIts nice to to think that all you care about is the realized return and totally avoid the path dependent nature of pretty much all returns today (even your own Personal Account, which gets Reg T treatment, and shut down if you don't post requisite collateral.).
ReplyDeleteReturn per unit of realised risk is how money management is assessed today. Then there is the ISDA, which measures expected risk and exchanges collateral based on each day's m-t-m risk. Most importantly there are fairly deep markets in variance and correlation, which can hedge these risks.
So just like realized return, there is also realized risk, which are both just single draws from a distribution which we will hardly know with anything like perfect foresight. However both matter with pretty much equal importance. Try to raise money by promising 15% return with 45% p/l volatility and see what happens!
Anyway this is a good post!
P.S. About the only thing that might get around the issue of realized risk is trading you own in a cash account (no leverage). Even then you should be comparing this to return per unit of risk and taking your own temperature from time to time.
Risk has a probability.
ReplyDeleteProbabilities can be measured.
Returns on investment are a function of demand, they are conditional on the state of the economy. In a demand shock recession, returns may drop due to slack demand and over capacity. While returns can be measured in the present, returns in the future cannot. They have risk, or a probability of being over or under estimate.
Investment decisions are based on rate of return and demand. This is where monetary policy runs into difficulty at the ZLB. Monetary policy can increase the rate of return if interest rates are lowered. But the returns cannot be realized if demand is slack. Fighting a recession at the ZLB requires restoration of demand before investors will risk investment in new or additional production.
-jonny bakho
You are getting at something I pointed out to Noah and the other (academics I think :-) ). BOTH return and risk are parameter draws from a realised distribution. We cannot know with any foresight (at least systematically) what these are going to be.
DeleteIt is true that you can pretend that return is simply [P(T)/P(0) - 1]. However what if we say that actual leverageable return is really [P(T)/P(0) - 1]/Sigma(0,T)? (Instead of Sigma you can use any other measure of dispersion)
In fact that is how the investment eco-system works! Also I think human behaviour works the same way. Highly volatilie wealth will make people behave very differently than more stable wealth.
Noah, you have to have this all wrong.
ReplyDeleteOur "Makers" have to be able to measure risk. Otherwise how can they be expected to function? We all know how very very sensitive to uncertainty our super heroic makers are. But you did not think about that, did you ?
I expect a retraction ! Wake up !
Noah,
ReplyDeleteYou have plotted nearly 30 years of volatility and are troubled by spikes probably lasting in months, and in that time, millions of contracts on S&P were traded... probably valued in multi-billions of dollars.
I think you are trying to formalize something that is unrealistic at the time scale you have chosen.
While it's true that we can't get a picture of historical (or prospective) risk just by looking at a price chart, perhaps we could get a better idea by having a model of the fundamentals of the asset? For instance, if you know that GM is basically a stable machine that turns out 5 million cars a year and sells them to 5 million people, you can sensibly say that it's lower risk than a defense contractor or an investment bank specialising in IPOs, which do 10 deals a year but make a billion dollars (or lose half a billion) on each of them.
ReplyDeleteOf course there are external factors you can't predict, such as a Toyota recall or a downturn in availability of cheap auto finance. But you can probably still say that Wal-Mart is lower risk than Goldman, or at least is likely to have lower variance in its daily price or quarterly profits.
Not that I disagree with your philosophical point, I just might moderate the claim a little.