The equation at the core of modern macro

I recently attended the Fall Conference at the Federal Reserve Bank of St. Louis. It was am excellent conference, with some of the world's most prominent macroeconomists presenting papers - Mike Woodford, Larry Christiano, Martin Eichenbaum, and Nancy Stokey (who was quite amused when I told her she was "one of the founders of behavioral finance"), among others. Bob Lucas, father of modern macro was in attendance, as were fellow bloggers Mark Thoma, David Andolfatto, and Steve Williamson. It was also great to meet the St. Louis Fed's charismatic leader, Jim Bullard.

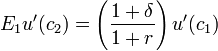
A lot of interesting papers were presented, but my favorite talk was by Martin Eichenbaum, who is by far the most fun econ seminar speaker I've ever seen. Along with his frequent co-author Christiano, Eichenbaum has taken on the task of making the gigantic "kitchen-sink" macro model that (hopefully) incorporates all of the various "frictions" and "shocks" that the macro community has decided are important for explaining business cycles. Whereas most macro models focus only on one or two features of the economy, Christiano and Eichenbaum and their various co-authors lump them all into one. In 2005, they came out with the Christiano-Eichenbaum-Evans model, which was the basis for the later Smets-Wouters model that has become the standard at central banks. Now they are offering a new and improved version, the Christiano-Eichenbaum-Trabandt model. This model relies much less on price stickiness to produce business cycles, and more on the labor-search models that have become popular since they won the Nobel Prize in 2010. 

But during his talk, Eichenbaum said something that really caught my attention: "Maybe next time [we update our model], we can finally get rid of the...Euler Equation."

For the uninitiated, the Consumption Euler (pronounced "oiler") Equation is sort of like the Flux Capacitor that powers all modern "DSGE" macro models. Here's a simple two-period version of it:

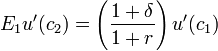
Basically, it says that how much you decide to consume today vs. tomorrow is determined by the interest rate (which is how much you get paid to put off your consumption til tomorrow), the time preference rate (which is how impatient you are) and your expected marginal utility of consumption (which is your desire to consume in the first place). When the equation appears in a macro model, "you" typically means "the entire economy".

This equation underlies every DSGE model you'll ever see, and drives much of modern macro's idea of how the economy works. So why is Eichenbaum, one of the deans of modern macro, pooh-poohing it?

Simple: Because it doesn't fit the data. The thing is, we can measure people's consumption, and we can measure interest rates. If we make an assumption about people's preferences, we can just go see if the Euler Equation is right or not!

When I caught up with him later, Eichenbaum was kind enough to refer me to the literature that tries to compare the Euler Equation to the data. The classic paper is Hansen and Singleton (1982), which found little support for the equation. But Eichenbaum also pointed me to this 2006 paper by Canzoneri, Cumby, and Diba of Georgetown (published version here), which provides simpler but more damning evidence against the Euler Equation.

Basically, in the Euler Equation, the interest rate "r" is supposed to be the safe interest rate. Canzoneri et al. look at money market funds, which are basically safe, and compare their interest rates to the rates predicted by the Euler Equation. What they find is a bit startling: there is a negative correlation between the two:

In other words, the Euler Equation says that if interest rates are high, you put off consumption more. That makes sense, right? Money markets basically pay you not to consume today. The more they pay you, the more you should keep your money in the money market and wait to consume until tomorrow.

But what Canzoneri et al. show is that this is not how people behave. The times when interest rates are high are times when people tend to be consuming more, not less. 

OK, but what about that little assumption that we know people's preferences? What if we've simply put the wrong utility function into the Euler Equation? Could this explain why people consume more during times when interest rates are high?

Well, Canzoneri et al. try out other utility functions that have become popular in recent years. The most popular alternative is habit formation, which Christiano, Eichenbaum, and Evans use in their 2005 model. But when Canzoneri et al. put in habit formation, they find that the Euler Equation still contradicts the data:

The negative correlation is harder to see in that picture, but it's still there.

Canzoneri et al. experiment with other types of preferences, including the other most popular alternative, Epstein-Zin preferences, and they find that the negative correlation never goes away. No matter what we assume that people want, their behavior is not consistent with the Euler Equation. Maybe if we kept trying different utility functions, we'd eventually find one that was less glaringly contradicted by the data...but as my macro teacher Chris House once told me, that is sort of an iffy thing to do. Maybe it's just the case that the economy doesn't make consumption decisions the way the Euler Equation says it does, and no funky preferences will fix the problem.

So anyway, what should we take away from this paper? Two things, I think.

1. If this paper is right - and one paper is not enough to be conclusive - then essentially all modern DSGE-type macro models currently in use are suspect. The consumption Euler Equation is an important part of nearly any such model, and if it's just wrong, it's hard to see how those models will work. If you have misspecified microfoundations, especially big stuff like this, it's going to make your model come out wrong. So more people need to be doing research to figure out if Euler Equations are, in fact, FUBAR.

2. I've often thought that macroeconomists should be more careful about checking their "intermediate results". In other words, macro theorists tend to make a bunch of assumptions, throw a bunch of equations into a model, see what comes out at the end, and then (loosely) compare those final results to the data. But usually, those equations lead to smaller-scale "intermediate results" that can be tested directly. This Euler Equation is an example. I say, test the parts, not just the whole. Why not?

I have to say that I was really, really impressed by Eichenbaum criticizing the Euler Equation (which he uses in his models) and referring me to a paper that specifically rebuts his most famous paper. First of all, it means he's willing to engage with critics, which is great. But even more importantly, it showed the kind of respect for the data that I've rarely seen in the macro field. Eichenbaum uses Euler Equations in his models because they're the only game in town, but he hopes to replace them someday, because they just don't seem to fit the facts. Eichenbaum really made me feel a lot better about the macroeconomics field; there really are macro people out there who aren't resigned to the defeatist idea that "all models are wrong"!

Updates: 

It's important to realize that there are other things that the authors don't consider that might work against the paper's result. Patrick Kehoe and Andrew Atkeson claim to have one here. Like I said, one paper is not enough; we need a whole literature of papers analyzing whether the Euler Equation is usable or not. Like Shiller's "excess volatility" result, it's going to take time before the weight of evidence piles up.

Carola Binder, over at her blog, points out that consumption Euler Equations are also extensively used in asset pricing models. This is true, and it is essentially impossible to talk to people in the asset pricing field without hearing people complain about this fact! Which is, of course, what prompted me to write this post in the first place...

Here is another (great) paper attacking the Euler Equation, which I had never seen. This paper basically finds that the equations are impossible to estimate. That casts a lot of doubt on the literature that is dedicated to estimating them.